Research


Preparing quantum states with measurements

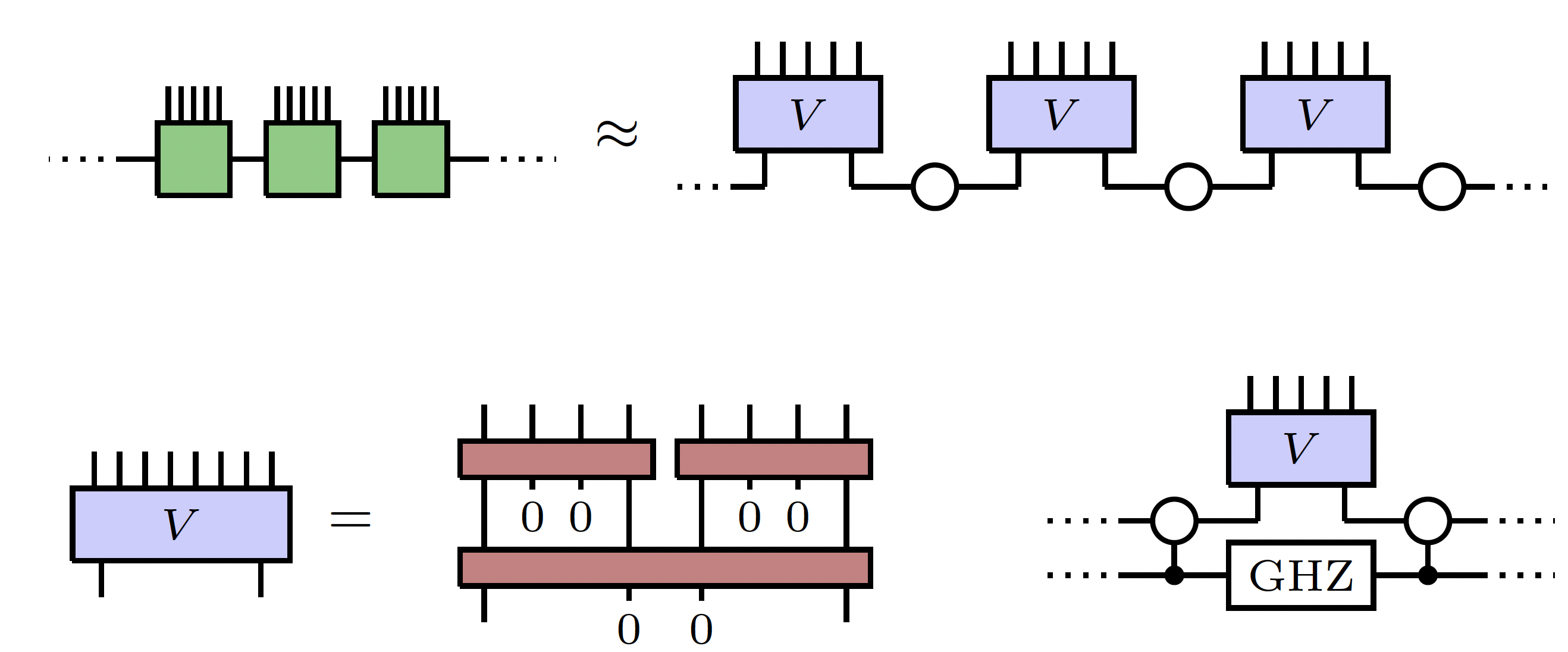
image
Algorithm to prepare a matrix-product state. Figure from PRL (2024).

Measurements are often solely thought of as means to extract information from a quantum state. However, measurement can also be used as an active ingredient in quantum protocols. This line of work explores how the resources (such as circuit depth) needed to transform a given state to a target one can be drastically reduced by utilizing measurements.

The problem of state preparation is evidently motivated by the practical need to prepare states in quantum devices, e.g., for quantum computing and simulation. However, it also has a more fundamental flavor to it since it connects to the classification of topological phases. It turns out that measurements can significantly lower the complexity for the preparation of states, which implies that certain topological phases collapse when measurements are considered.


Selected Publications:


  • Characterizing MPS and PEPS Preparable via Measurement and Feedback,
    Zhang, Gopalakrishnan, Styliaris [PRX Quantum (2024)]

  • Approximating many-body quantum states with quantum circuits and measurements,
    Piroli, Styliaris, Cirac [PRL (2024)]


  • Phases of Matrix Product States with Symmetric Quantum Circuits and Symmetric Measurements with Feedforward,
    Gunn, Styliaris, Kraft, Kraus [arXiv (2023)]



Exactly solvable quantum states and dynamics

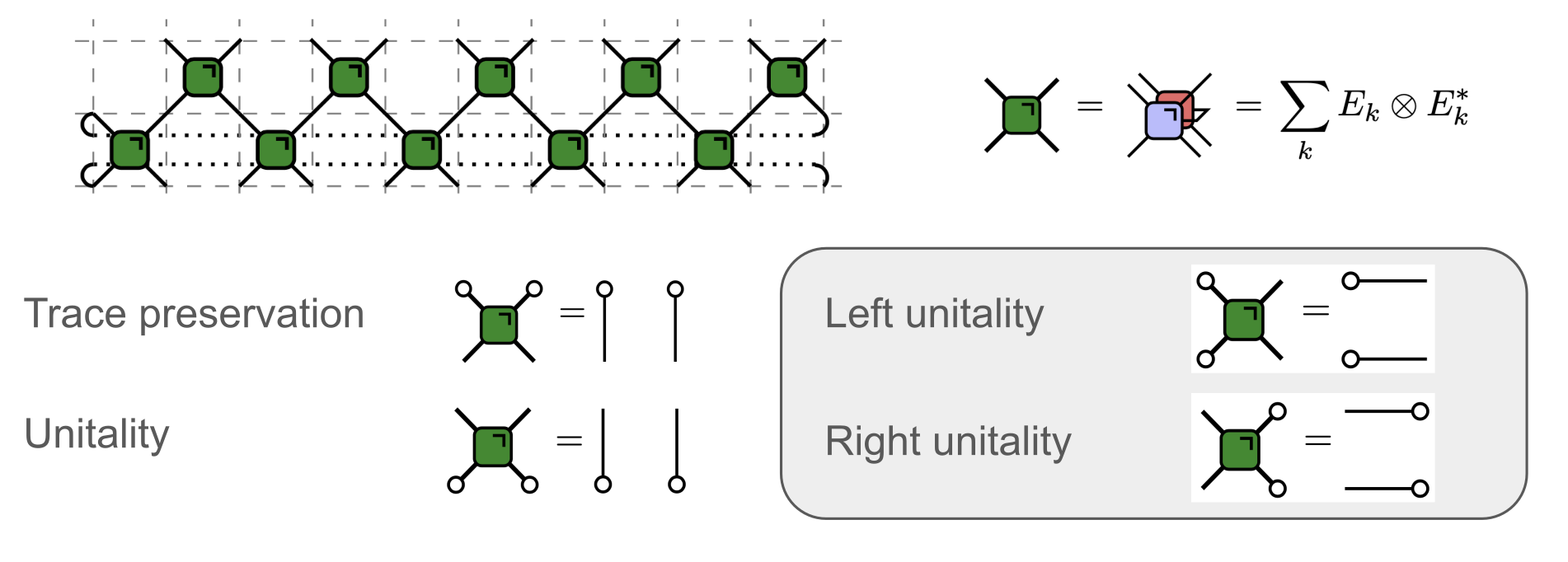
image
A quantum circuit of space-time quantum channels. Figure from Quantum (2023).

Dual-unitary circuits have emerged as a rich model of quantum dynamics. While this class includes both integrable and chaotic models, it allows for the analytical solution of correlation functions. The defining property of these circuits is that, when the role of space and time is exchanged, the corresponding evolution remains physical, i.e., unitary.

No realistic quantum system is perfectly isolated. Fortunately, it turns out that the ideas of dual-unitarity can be extended to the realm of open systems. Here we explore how, by postulating the analogous symmetry between space and time, solvability is extended to quantum channels.

The same ideas allow to define a nontrivial subclass of 2D tensor-network states with exactly solvable single and 2-body correlation functions. The connection can be understood by interpreting the tensor-network contraction as evolution over the virtual space.


Selected Publications:


  • Dual-isometric Projected Entangled Pair States,
    Yu, Cirac, Kos*, Styliaris* [PRL (2024)]



Theory of tensor networks

image
Multiple copies of a random tensor network. Figure from PRX Quantum (2023).

The many-body Hilbert space is large, as it grows exponentially with the number of constituents [“no one can hear you scream there”, as I learned from Todd Brun]. However, when interactions are local, the corresponding low-energy eigenstates are captured by tensor-networks. This not only allows for an efficient description of the relevant quantum states, but also provides a general framework for many-body physics, in the language of quantum information.


Selected Publications:


  • Matrix-product unitaries: Beyond quantum cellular automata,
    Styliaris, Trivedi, Pérez-García, Cirac [arXiv (2024)]

  • Typical Correlation Length of Sequentially Generated Tensor Network States,
    Haag, Baccari, Styliaris [PRX Quantum (2023)]


Quantum information theory & Quantum computing

image
Symmetries in Markovian dynamics give rise to monotones. Figure from Quantum (2020).

Quantum information offers a powerful language for understanding quantum phenomena through the lens of information processing and computation. I enjoy thinking about different problems from the perspective of quantum information, ranging from measurement incompatibility, to information scrambling and symmetries in open systems.


Selected Publications:


  • Accuracy guarantees and quantum advantage in analogue open quantum simulation with and without noise,
    Kashyap, Styliaris, Mouradian, Cirac, Trivedi [arXiv (2024)]

  • Computable Rényi mutual information: Area laws and correlations,
    Scalet, Alhambra, Styliaris, Cirac [Quantum (2021)]

  • Information Scrambling over Bipartitions: Equilibration, Entropy Production, and Typicality,
    Styliaris, Anand, Zanardi [PRL (2021)]

  • Symmetries and monotones in Markovian quantum dynamics,
    Styliaris, Zanardi [Quantum (2020)]

  • Fundamental Limitations to Local Energy Extraction in Quantum Systems,
    Alhambra, Styliaris, Rodríguez-Briones, Sikora, Martín-Martínez [PRL (2019)]

  • Quantifying the Incompatibility of Quantum Measurements Relative to a Basis,
    Styliaris, Zanardi [PRL (2019)]